JEE Main Cartesian Co-ordinate System - Key Point Question Answers

Centroid: The co-ordinates of centroid of the triangle whose vertices are (x₁, y₁), (x₂, y₂) and (x₃, y₃) are:

( x₁ + x₂ + x₃ 3 , y₁ + y₂ + y₃ 3 )

The point of concurrency of the medians called the centroid of the triangle

In-center of a triangle

The point of concurrency of the internal bisectors of the angles of a triangle is called the incentre of the triangle.

The co-ordinates of the incentre of a triangle with vertices A(x₁, y₁), B(x₂, y₂) and C(x₃, y₃) are:

( ax₁ + bx₂ + cx₃ a + b + c , ay₁ + by₂ + cy₃ a + b + c )

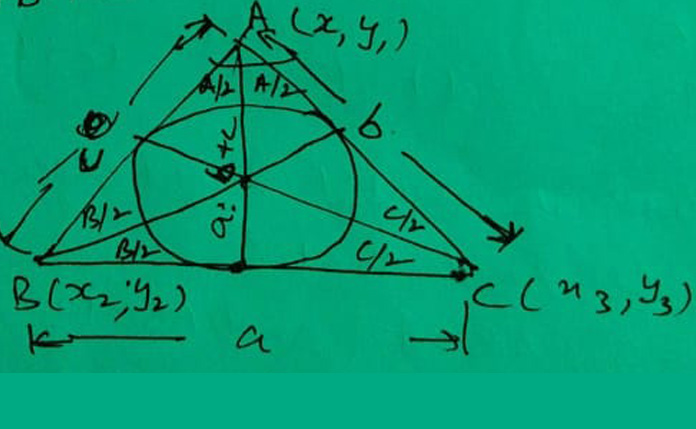
Note: In an equilateral triangle, incentre cobncide with the centriod,

Ques. The incentre of the triangle with vertices (1, √3), (0, 0) and (2, 0) is:

(a.)

(1, √3/2)

(b.)

(2/3, 1/√3)

(c.)

(2/3, √3/2)

(d.)

(1, 1/√3)

Solution:

A(1, √3) B(0, 0) C(2, 0)

AB = 2 = BC = AC

The triangle is equilateral, its incentre concides with the centroid whose co-ordinates are:

( 1 + 0 + √2 3 , √3 + 0 + 0 3 )

= (1, 1/√3)

Ques. The incentre of the triangle having its vertices at O(0, 0), A(5, 0) and B(0, 12) is:

(a.)

(3, 3)

(b.)

(2, 2)

(c.)

(7, 7)

(d.)

(9, 9)

Solution:

∆ OAB is right angled at 0 such that

OA = 5, OB = 12 and AB = 13

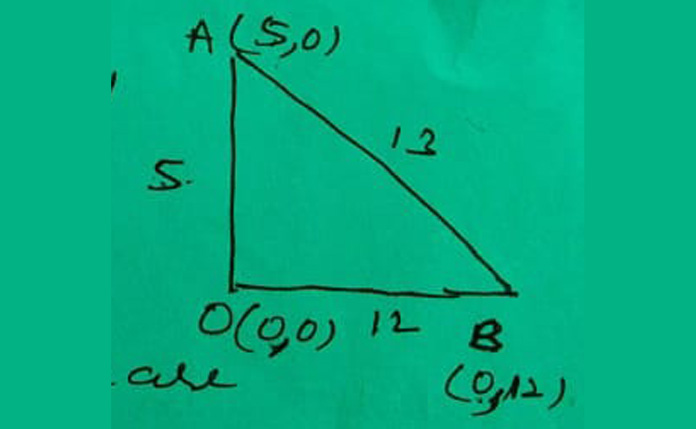
So, the co-ordinates of incentre are

( 13x0 + 5x0 + 12x5 13 + 5 + 12 , 13x0 + 5x12 + 12x0 13 + 5 + 12 )

i.e. (2, 2)

If D(x₁, y₁), E(x₂, y₂) and F(x₃, y₃) are mid points of the sides BC, CA and AB respectively of ∆ABC. Then, the co-ordinates of vertices are A(x₂ + x₃ - x₁, y₂ + y₃ - y₁), B(x₃ + x₁ - x₂, y₃ + y₁ - y₂) and C(x₁ + x₂ - x₃, y₁ + y₂ - y₃)

Ques. The x-coordinate of the incentre of the triangle that has the coordinates of mid points of its sides are (0, 1), (1, 1) and (1, 0) is:

(a.)

2 + √2

(b.)

2 - √3

(c.)

1 + √2

(d.)

1 - √2

Solution:

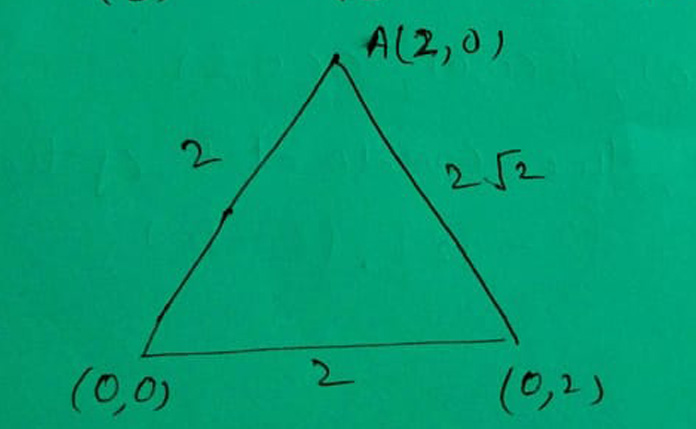
In the given problem the coordinates of mid points are D(0, 1), E(1, 1) and F(1, 0).

So the coordinates of vertices are A(2, 0), B(0, 0) and C(0, 2).

∴ Coordinates of the incentre are

( 2x2 + 2√2x0 + 2x0 2 + 2√2 + 2 , 2x0 + 2√2x0 + 2x2 2 + 2√2 + 2 )

( 2 2√2 , 2 2√2 )

(2 - √2, 2 - √2)

Ques. The x-coordinate of the incentre of the triangle where the mid points of the sides are (0, 1), (1, 1) and (1, 0) is:

(a.)

2 + √2

(b.)

1 + √2

(c.)

2 - √2

(d.)

1 - √2

Solution:

Let D(0, 1), E(1, 1) and F(1, 0) be the mid points of sides BC, CA and AB respectively of ∆ABC. Then the coordinates of the vertices are

A(1 + 1 - 0, 0 + 1 - 1), B(0 + 1 - 1, 1 + 0 - 1), C(0 + 1 - 1, 1 + 1 - 0)

A(2, 0), B(0, 0) and C(0, 2)

Hence, the coordinates of the incentre

are (2 - √2), (2 - √2)

If a vertex of a triangle is (1, 1) and the mid points of two sides through this vertex are (-1, 2) and (3, 2), then the centroid of the triangle is:

(a.)

(1/3, 7/3)

(b.)

(1, 7/3)

(c.)

(-1/3, 7/3)

(d.)

(-1, 7/3)

Solution:

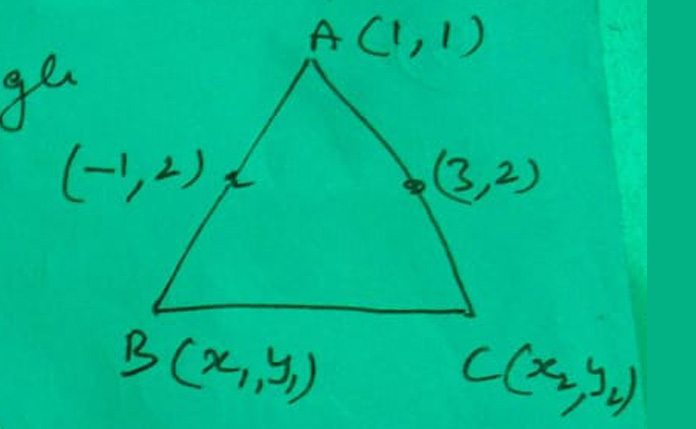
Let ABC be the given triangle whose vertices are A(1, 1), B(x₁, y₁) and C(x₂, y₂).

Let D(-1, 2) and E(3, 2) be the midpoints of AB and AC then

(x₁ + 1)/2 = -1, (y₁ + 1)/2 = 2

=> x₁ = -3

=> y₁ = 3

(x₂ + 1)/2 = 3 => x₂ = 5

(y₂ + 1)/2 = 2 => y₂ = 3

∴ the coordinates of the vertices of ∆ABC are A(1, 1), B(-3, 3) and C(5, 3)

∴ centroid

( 1 - 3 + 5 3 , 1 + 3 + 3 3 )

= (1, 7/3)

Circum circle and circum centre (o)

=> The circle passes through the angular point of a ∆ABC is called its circum circle where perpendicular bisectors of the sides are concurrent. Circum centres of acute angles triangle and obtuse angled triangle lie inside and outside of the triangle respectively.

Circum centre of right angled triangle is mid point of hypotnuse.

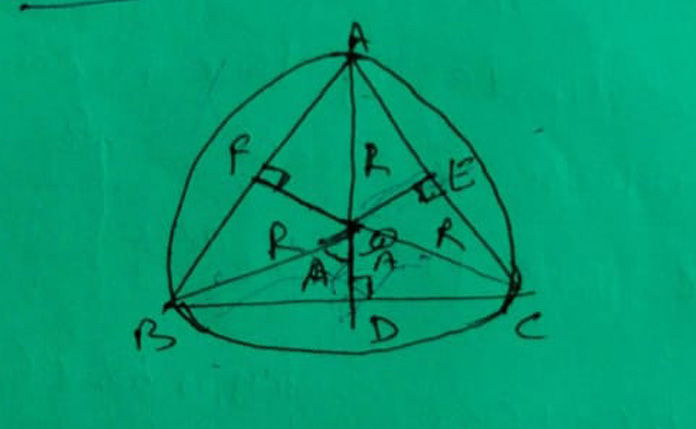
Distance of circum centre from sides

OD = R cosA, OE = R cosB and OF = R cosC

R - The radius of the circum circle of the triangle.

In-circle and in-centre (I)

The point of intersection of internal bisectors of triangle is incentre of triangle which is the centre of the circle touching all the three sides internally, Incentre always lies inside the triangle.

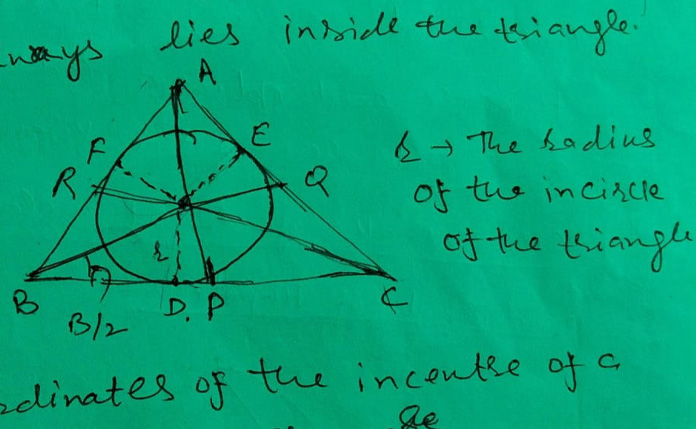
The co-ordinates of the incentre of a triangle whose vertices are (x₁, y₁), (x₂, y₂) and (x₃, y₃) are

I( ax₁ + bx₂ + cx₃ a + b + c , ay₁ + by₂ + cy₃ a + b + c )

Orthocentre of the triangles is the intersection of the altitudes drawn from the vertices of the triangle to the opposite sides. For an acute ∆, it lies inside the triangle. For an obtuse triangle, its lies outside of triangle. For a right-angled triangle, it lies on the vertex of the right angle.

Ques. The vertices of a triangle are at O(0, 0), A(a, 0) and B(0, b). The distance between its circumcentre and orthocentre is:

(a.)

√(a² + b²)

(b.)

1/2 √(a² + b²)

(c.)

√(a² + b²)/2

(d.)

1/4 √(a² + b²)

Solution:

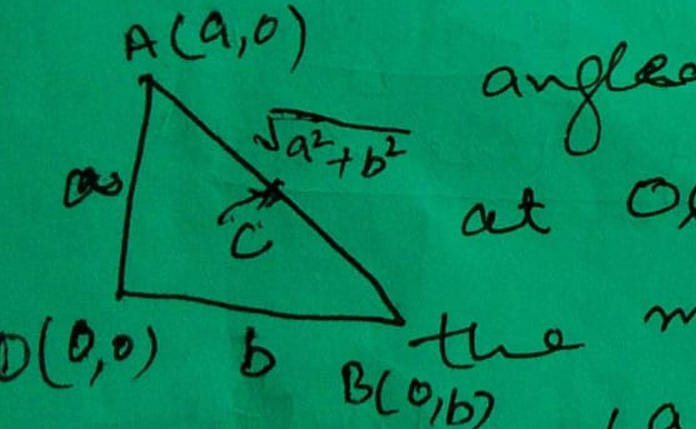
∆ OAB is right angled triangle right angled at O. So its orthocentre is at O(0, 0) and circumcentre is the mid point of its hypotnuse i.e. C(a/2, b/2)

∴ Required distance = √[(a/2 - 0)² + (b/2 - 0)²]

= 1/2 √(a² + b²)

Key Points

=> In right angled triangle, right angled at O(0, 0) and orthocentre is (0, 0), circum centre is the mid points of its hypotnuse.

=> In an equilateral triangle, its incentre coincides with the centroid, coordinates of incentre and centroid are same.

=> In right angled triangle orthocentre lies on the vertex of a right angle.

=> Circumcentre(O), G(centroid) and H(x, y). Orthocentre are collinear such that G divides OH in the ratio 1:2

Key Points

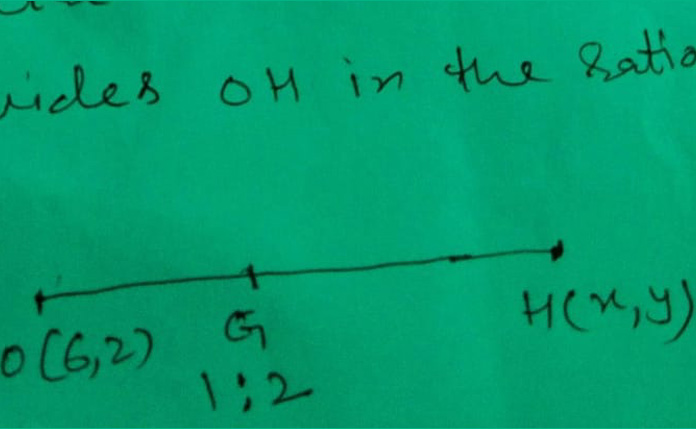
Circumcentre: Perpendicular bisectors of the sides are concurrent known as circumcentre.

Circumcentre of right angled triangle is the mid point of hypotenuse.

Ques. Coordinates of the vertices of a triangle ABC are (12, 8), (-2, 6) and (6, 0) then the correct statement is:

(a.)

Triangle is right but not isosceles

(b.)

Triangle is isosceles but not right

(c.)

Triangle is obtuse

(d.)

The product of the abcissa of the centroid, or two centre and circumcentre is 160

Solution:

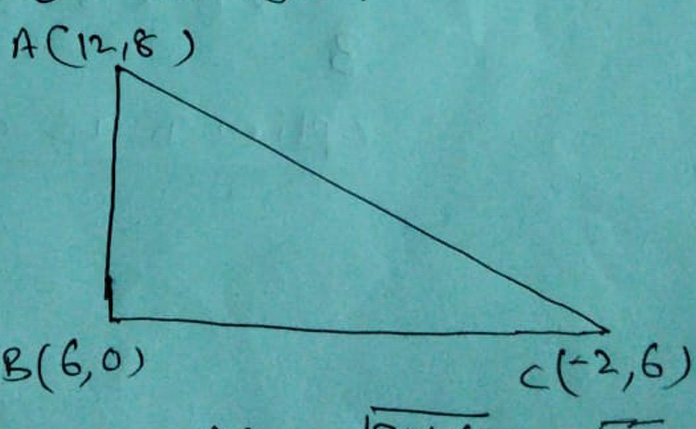
AB = √(36 + 64) = √100

BC = √(36 + 64) = √100

AC = √(4 + 196) = √200

AC² = AB² + BC²

(√200)² = (√100)² + (√100)²

200 = 100 + 100 = 200

∴ ∆ABC is a right angled ∆ at B.

In right angled ∆ orthocentre lies on the vertex of a right angle i.e. at B and circumcentre is the mid point of its hypotnuse i.e. [(-2 + 12)/2, (8 + 6)/2] or O(5, 7)

Centroid = G[(12 + 6 - 2)/3, (8 + 0 + 6)/3]

= G(16/3, 14/3)

∴ Product of abcissa of centroid, orthocentre and circumcentre is

= (16/3)x6x5

= 160

Option D is correct

Key Points

Circumcentre O, centroid G and orthocentre H of an acute ∆ ABC are collinear. G divides OH in the ratio 1:2 i.e. OG:GH = 1:2

In an isosceles triangle, centroid, orthocentre, incentre and circumcentre lie on the same line. In an equilateral triangle, all these four points coincide.

Ex. If the centroid and circumcentre of a triangle are (3, 3) and (6, 2) respectively, then the orthocentre is

(a.)

(-3, 5)

(b.)

(-3, 1)

(c.)

(3, -1)

(d.)

(9, 5)

Solution:

O(6, 2) -> circumcentre, G(3, 3) -> centroid and H(x, y) -> orthocentre are collinear such that G divides OH in the ratio 1:2

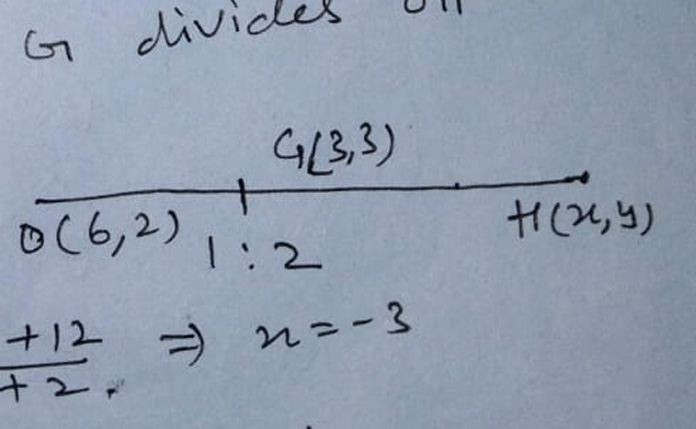
∴ 3 = (x + 12)/(1 + 2) => x = -3

and 3 = (y + 4)/(1 + 2) => y = 5

∴ The co-ordinates of orthocentre are (-3, 5)

Ques. If the circumcentre of a triangle lies at the origin and the centroid is the middle point of the line joining the points (a² + 1, a² + 1) and (2a, -2a) the orthocentre statistics the equation.

Solution:

The circumcentre is at the origin and the centroid is at

{(a² + 1 + 2a)/2, (a² + 1 - 2a)/2}

i.e at {(a + 1)²/2, (a - 1)²/2}

Let (x, y) be the orthocentre, Since centroid divides the line segment joining circumcentre and orthocentre in the ratio 1:2

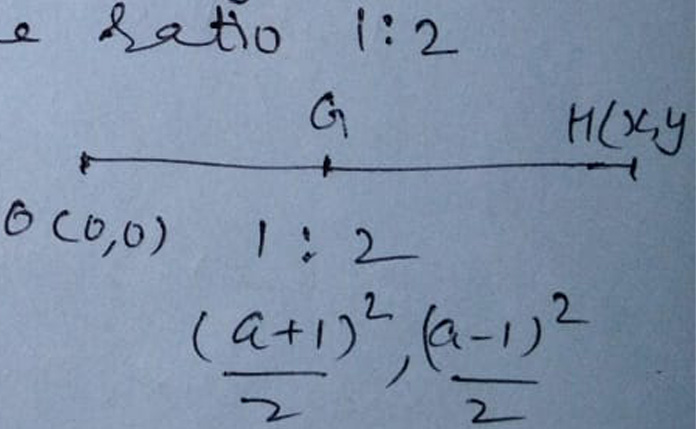
(a + 1)²/2 = x/3 -(1)

(a - 1)²/2 = y/3 -(2)

Dividing 1 and 2

(a + 1)²/(a - 1)² = x/y

=> (a - 1)²x = (a + 1)²y

Ques. Let the orthocentre and centroid of a triangle be A(-3, 5) and B(3, 3) respectively. If C is the circumcentre of this triangle, then the radius of the circle having line segment AC as diameter is:

(a.)

2√10

(b.)

3√(5/2)

(c.)

(3√5)/2

(d.)

√10

Solution:

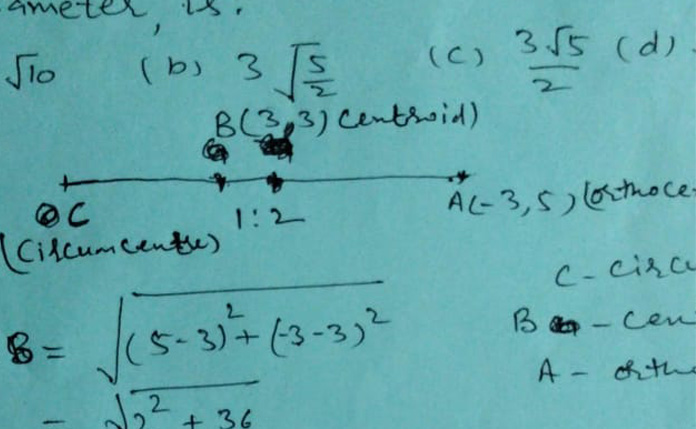
C - Circumcentre

B - Centroid

A - Orthocentre

∴ AB = √{(5 - 3)² + (-3 - 3)²}

= √(2² + 36)

= √40

= 2√10

∴ AC = (3/2)AB

= (3/2) x 2√10

= 3√10

Hence radius = (3/2)√10

= 3{√(10/4)}

= 3{√(5/2)}

Key Concept

Ques. If the circumcentre of the triangle formed by points (0, 0), (2, -1) and (-1, 3) is at (5/2, 5/2), then the cordinates of its orthocentre are:

(a.)

(-4, -3)

(b.)

(4, 3)

(c.)

(-4, 3)

(d.)

none of these

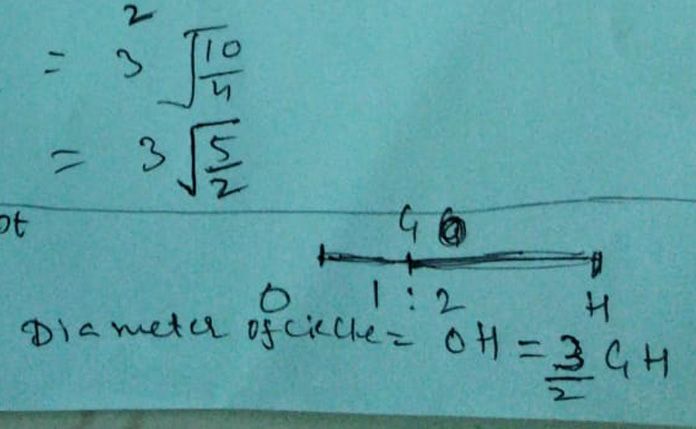
Solution:

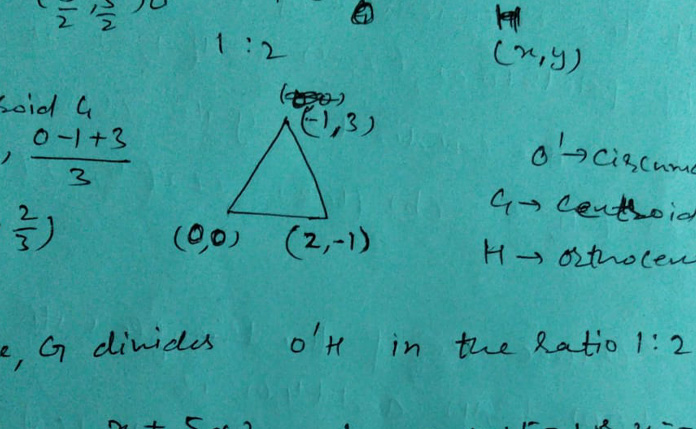
O' - Circumcentre

G - Centroid

H - Orthocentre

O'(5/2, 5/2)

G(1/3, 2/3)

H(x, y)

Centroid G = {(0 + 2 - 1)/3, (0 - 1 + 3)/3} = G(1/3, 2/3)

Hence G divides O'H in the ratio 1:2

[{x + (5/2)x2}/3] = 1/3

=> x + 5 = 1 or x = -4

{y + 2x(5/2)}/3 = 2/3

=> y + 5 = 2 => y = -3

∴ H(-4, 3)

Ques. Orthocentre of the triangle with vertices (0, 0), (3, 4) and (4, 0) is:

(a.)

(3, 5/2)

(b.)

(3, 12)

(c.)

(3, 3/4)

(d.)

(3, 9)

Solution:

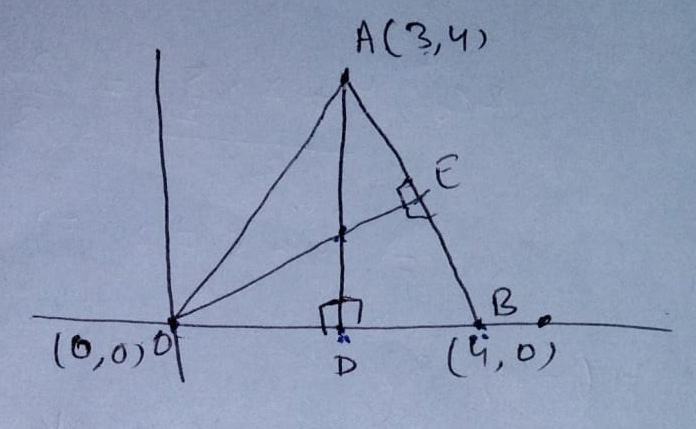
We know that orthocentre is the meeting point of altitudes of a ∆

Equation of altitude AD

AD is line ∥ to y-axis through(3, 4)

=> x = 3 -(1)

Equation of OE.

OE passes through (0, 0) and is perpendicular to AB

y = (1/4)x -(2)

∴ from (1) and (2)

We get orthocentre as (3, 3/4)

Ques. The circumcentre of the triangle with vertices (0, 0), (3, 0) and (0, 4) is:

(a.)

(1, 1)

(b.)

(2, 3/2)

(c.)

(3/2, 2)

(d.)

None of these

Solution:

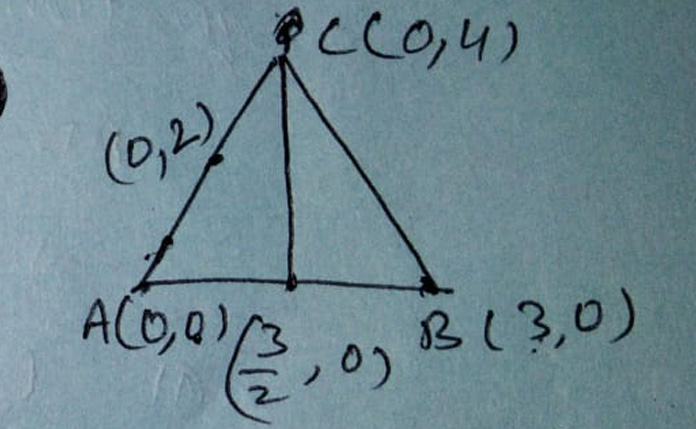
Mid point of AB = (3/2, 0)

x = 3/2 is the equation of bisectors of AB

Mid point of AC = (0, 2)

Equation of bisectors of AC is y = 2

(3/2, 2) is the circumcentre of required ∆

Ques. Two vertices of a triangle are (0, 2) and (4, 3). If its orthocentre is at the origin then its third vertex lies in which quadrant?

(a.)

Fourth

(b.)

Second

(c.)

Third

(d.)

First

Solution:

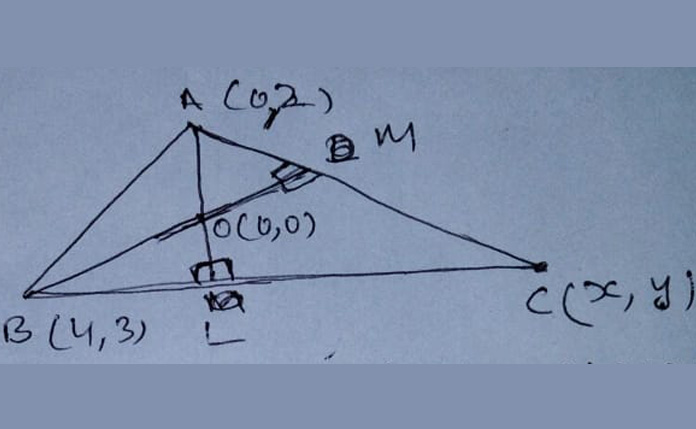
Let C(x, y) be the third vertex of ∆ABC.

Let AL and BM be two altitudes of ∆ABC. It is given that O(0, 0) is the orthocentre of ∆ABC

∴ OA ⊥ BC and OB ⊥ AC

=> BC is parallel to x-axis and slope OB x slope of AC = -1

=> y - 3 = 0 and [{3/4} x {(b - 2)/(a - 0)}] = -1

=> y = 3 and 4a + 3b = 6

b = 3, and a = -3/4

Clearly, C(a, b) = (-3/4, 3)

Key Point

Conjugate Harmonic Function:

If f(2) = 4 + iv is an analytics finction, then "v" is the conjugate harmonic of "u" and vice versa.

If f(z) = u + iv is an analytical function, then f(z) = -v + iu, u and v are harmonic conjugates.

Q. If p(3, 7) is a point on the line joining A(1, 1) and B(6, 16) then harmonic conjugate Q of point P has the coordinate:

(a.)

(9, 19)

(b.)

(-9, 29)

(c.)

(9, -29)

(d.)

(-9, -29)

Solution:

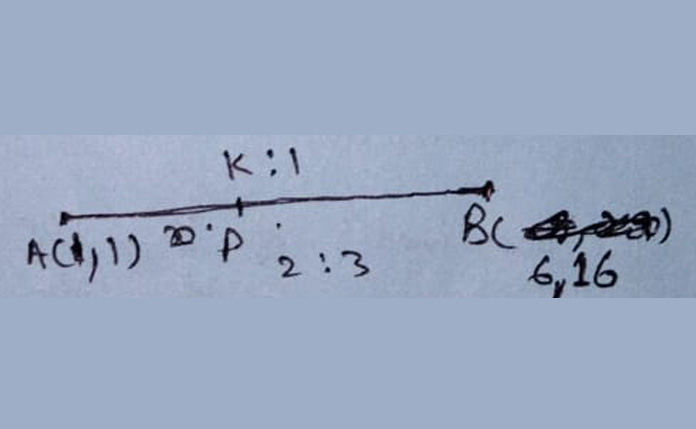
(6k + 1)/(k + 1) = 3 => 6k + 1 = 3k + 3 => k = 2/3

(16k + 1)/(k + 1) = 7

=> P divides AB internally in the ratio 2:3

Thus Q divides AB externally in the ratio 2:3 and hence its coordinates are

{(2x6 - 3x1)/(2 - 3), (2x16 - 3x1)/(2 - 3)}

= (-9, -29)

Q. The harmonic conjugate of (4, -2) with respect to (2, -4) and (7, 1) is:

(a.)

(-8, -14)

(b.)

(2, 3)

(c.)

(-2, -3)

(d.)

(13, -5)

Solution:

Given points are P(-4, 2), A(2, -4) and B(7, 1)

Suppose P divides AB in ratio k:1, then

=> P divides AB internally in the ratio 2:3

Thus Q divides AB externally in the ratio 2:3 and hence its coordinates are

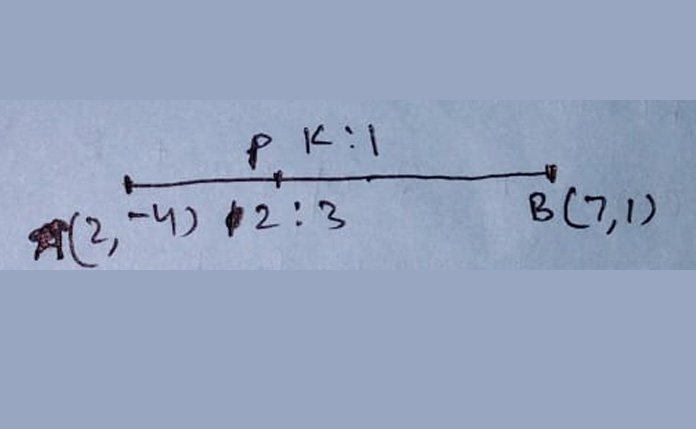
(7k + 2)/(k + 1) = 4 => k = 2/3

∴ P divides AB internally in the ratio 2:3

The coordinates of the point a dividing AB externally in the ratio 2:3 are

(2x7 - 3x2)/(2 - 3), (2x1 - 3x4)/(2 - 3)

=(-8, -14)

Hence the harmonic conjugate of R with respect to A and B is (-8, -14)

Key Point: Family of lines:

Let L1 = a₁x + b₁y + c₁ = 0 and

L2 = a₂x + b₂y + c₂ = 0

then the equation of the lines passing through the point of intersection of these lines is

L₁ + λL₂ = 0 where λ ∈ R

These lines from a family of straight lines from point P.

Also this general equation satisfies the point of intersection of L₁ and L₂ for any value of λ is obtained with the help of the addiotional information given in the problem.

Q. Find the straight line passing through the point of intersection of 2x + 3y + 5, 5x - 2y - 16 = 0 and through the point (-1, 3).

Solution:

The equation of any line through the point of intersection of the given line is

2x + 3y + 5 + λ(5x - 2y - 16) = 0 - (1)

But the required line passes through (-1, 3)

∴ Weget

-2 + 9 + 5 + λ(-5 - 6 - 16) = 0

Hence, λ = 4/9 - (2)

∴ From 1 and 2

2x + 3y + 5 + 4/9(5x - 2y - 16) = 0

=> 9(2x + 3y + 5) + 4(5x - 2y - 16) = 0

Simplifying, we get

2x + y - 1 = 0

Q. Show that the straight lines x(a + 2b) + y(a + 3b) = a + b for different values of a and b pass through a fixed point. Find that point

Solution:

Given equation is

x(a + 2b) + y(a + 3b) = a + b

=> a(x + y - 1) + b(2x + 3y - 1) = 0 -(1)

Both a and b cannot be simultaneously zero.

∴ at least one a and b will be non-zero, let a ≠ 0

(1) can be written as

x + y - 1 + b/a(2x + 3y - 1) = 0

x + y + 1 + λ(2x + 3y - 1) = 0

where λ = b/a

From (2) it is clear that (2) passes through the point of intersection of lines x + y - 1 = 0, and 2x + 3y - 1 = 0 solving, weget x = 2, y = - 1

Hence the lines

Key Point:

If two vertices of an equilateral triangle have the co-ordinates (x₁, y₁) and (x₂, y₂), then the co-ordinates of its third vertex are:

[{x₁ + x₂ ± √3(y₁ - y₂)}/2, {y₁ + y₂ ± √3(x₁ - x₂)}/2]

Q. If the co-ordinates of two vertices of an equilateral ∆ are (2, 4) and (2, 6), then the coordinates of its third vertex is:

(a.)

(√3, 5)

(b.)

(2√3, 5)

(c.)

(2+√3, 5)

(d.)

(2, 5)

Solution:

{2 + 2 ± √3(-2)}/2, {10 ± √3(0)}/2

{4 ± √3(-2)}/2, 5

(2 ± √3, 5)